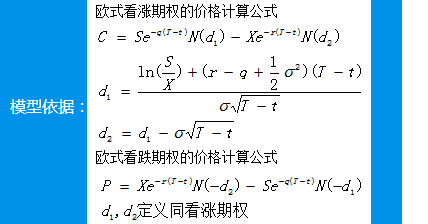说明
本实验依托Black-Scholes欧式期权定价公式,分析期权价格的六大影响因素——标的资产价格、执行价格、到期期限、无风险利率、标的资产波动率、便利收益率对期权价格的交叉影响,重点分析标的资产价格与到期期限,标的资产价格与波动率,标的资产价格与无风险利率、执行价格与波动率等双因素对期权价值的交互影响,因此本实验绘制的是三维动态关系图,可以通过拖动,选择合适的角度下载实验图片进行分析。
参数说明:
标的资产现价(S):单位为元;
执行价格(X):单位为元;
到期期限(T-t):单位为日,一年可设为360或365日;
无风险利率(r):单位为百分比,如利率5%,可输入:5
波动率(σ):单位为百分比,如20%,可输入20
便利收益率(红利率,q):单位为百分比,如利率5%,可输入:5
实验方法:(更详细的实验操作可以参考实验指导视频)
1)首先选择两个可变参数,每次实验选取其中两个参数。从应用价值而言,同时变动标的资产价格和标的资产波动率,或标的资产价格和到期期限、或执行价格和波动率更有意义。
2)设定其他参数的初始值,可以通过更改默认值来设定初始参数值,所有其他参数均需要有初始值。
3)设定两个可变参数的取值范围:最小值,最大值,以及区间的分段数量,如标的资产价格设为最小值10,最大值200,[10,200]内等分为100段。
4)选择期权类型:看涨 或 看跌。
5)点击”计算”按钮,即可以看到可变参数不同取值下期权的价格变化三维图。
注意:图形中所有数据点都可以跟随鼠标显示数据点的三维取值,方便记录分析。